F & F Koenigkramer barber chairs began in the 1920’s as a result of a business partnership that turned sour. These chairs are known for having the world’s first foot-operated hydraulic lift. They were later branded as Reliance barber chairs. Although they are not the main product of the company, they were still manufactured up until the 50’s and 60’s. During that era, a lot of barber chair companies went out of business due to the arrival of Japan-based Takara Belmont Company.
F & F stands for Fred and Frank. They are sons of William Koenigkramer, a German immigrant in the 1860’s. The brothers invented a clog-free paint sprayer which became a bestseller to farmers. Fred and Frank were also really good at engineering hydraulic lifts. They were so good that the pioneering barber chair company in the United States, Eugene Berninghaus Co., later approached them and forged a deal with them so that their hydraulic lifts can be integrated into the Berninghaus barber chairs. In the 1890’s, the two sons formed F & F Koenigkramer. It was a initially machine shop business based in Cincinnati, Ohio.
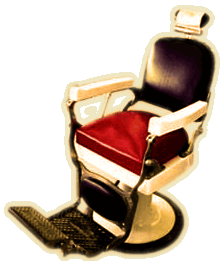
The 1920’s was a period of adjustment for the Koenigkramer brothers. First, the partnership between fellow German, Eugene Berninghaus, did not end up well. Business was booming for Eugene, and the brothers believed that the deal wasn’t fair. As a result, the deal was off and a new competing product was formed in the name of F. & F. Koenigkramer barber chairs.
At the end of the decade, a new opportunity came. The General Optical Company commissioned the brothers to build a set of medical equipment for its exclusive use. As with most companies in the country, production was temporarily stopped during World War II. After the war, F. & F. Koenigkramer decided to classify their medical products as belonging to the product line called, “Reliance.” As has been mentioned, the barber chairs were eventually adapted into it.
Due to intense competition, the company ultimately focused on medical equipment under the name, Reliance Medical Equipment. At this point, Koken Barber’s Supply Co. was purchased by Takara Belmont Co., and Emil J. Paidar Co. did not have the largest market share anymore in the barber’s supply business. In 1988, a company based in Bern, Switzerland acquired Reliance. Today, Haag-Streit AG has its manufacturing operations in Mason, Ohio. The same facility also houses the marketing department of Reliance and other sister companies.
I have a old chair up for sale. How much do they go for ?
I have a 1966 f & f koeningkramer reliance, barber chair ; I cannot figure out how to get it out of the locked position with the handle. Can someone please help me. thank you